1303. Ultra-QuickSort
In
this problem you have to analyze a particular sorting algorithm. The algorithm
processes a sequence of n distinct
integers by swapping two adjacent sequence elements until the sequence is
sorted in ascending order. For the input sequence
9
1 0 5 4
Ultra-QuickSort
produces the output
0
1 4 5 9
Your
task is to determine how many swap operations Ultra-QuickSort needs to perform
in order to sort a given input sequence.
Input. Consists
of several test cases. The first line of each test case contains the length of
the input sequence n (n ≤ 500,000). Each of the
following n lines contains a single
integer ai (0 ≤ ai ≤ 999,999,999), the i-th input sequence element. The last
test case contains n = 0 and is not
processed.
Output.
For every input sequence print a single line containing an integer number op – the minimum number of swap
operations necessary to sort the given sequence.
|
Sample
input |
Sample
output |
|
5 9 1 0 5 4 3 1 2 3 0 |
6 0 |
SOLUTION
sort - merge sort
Algorithm analysis
The
minimum number of swaps required to sort the given sequence equals to the
number of inversions in the input sequence. The desired number of inversions
can be found in time O(nlog2n) simulating the merge sort.
Consider
the merging process of two arrays A = (a1,
…, an) and B = (b1, …, bm). Let the parts A = (a1, …, ai-1)
and B = (b1, …, bj-1) are already
merged, and currently we compare the numbers ai and bj.
Let ai > bj, and the element bj is moved to the merged
array. Then we claim that bj
makes inversions only with elements ai,
…, an, and the number of
such inversions is exactly n – i + 1.
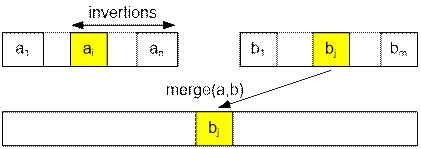
Example
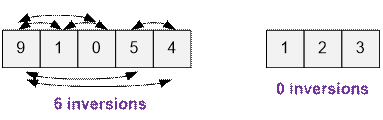
Count the number of
inversions in the first and in the second example.
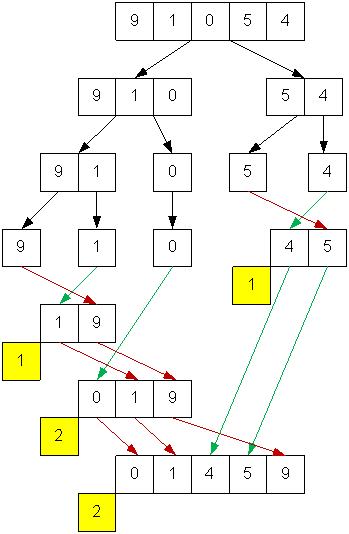
Let’s
simulate the merge sort from the first example. Inversions are counted during
the merge operation. Near each sequence obtained after merge operation, we give
the number of inversions formed by the elements of the merged subsequences.
Algorithm realization
Input sequence will be stored
in the array m.
int *m;
Merge
the sorted arrays a[bL] ... a[bR]
and a[cL]
... a[cR] into a[bL] ... a[cR]. Note that
we always have bR + 1 = cL. For merging
we use an additional array res.
void merge(int *a, int bL, int bR, int cL, int cR)
{
Put to len the number of elements being merged. Create an array res (a buffer),
into which the elements will be merged.
int i = 0, Left = bL, len = cR - bL + 1;
int *res = new int[len];
The currently viewed position in
the first sequence is bL, the currently
viewed position in the second sequence is cL.
That is, at each iteration, the values a[bL]
and a[cL] are compared. The lesser of
these values is copied to the buffer res. As more elements are added to the
buffer, the values of bL and cL are increased by 1. As soon as one of
them achieves the end of the sequence (bL
becomes greater than bR or cL becomes greater than cR), the loop terminates. It means that
all the elements of one of the merged sequence are copied completely to the
buffer.
The number of inversions swaps changes when we move the element
of the second sequence to the buffer. At the same time, the value swaps
is increased by the number of unmerged elements of the first sequence, that
equals to bR – bL + 1 (the elements a[bL
.. bR] from the first sequence are
not moved to the buffer yet).
while((bL <= bR) && (cL <= cR))
if (a[bL] <= a[cL]) res[i++] = a[bL++];
else res[i++] = a[cL++], swaps += bR -
bL + 1;
One of the merged sequences is
over. Copy the rest of the other sequence to the end of the buffer.
while (bL <= bR) res[i++] = a[bL++];
while (cL <= cR) res[i++] = a[cL++];
Copy all the contents of the
buffer to array à, beginning from the cell Left.
memcpy(a + Left,res,len*sizeof(int));
Remove the buffer – the whole
array res.
delete[] res;
}
Sort the array a[left
... right] using “divide and conquer”
algorithm. To do this, divide it into two parts a[left ... middle] and a[middle + 1 ... right], sort each of them separately, and then perform a merge.
void
mergeSort(int *a, int
left, int right)
{
if (left
>= right) return;
int middle =
(left + right) / 2;
mergeSort(a,left,middle);
mergeSort(a,middle+1,right);
merge(a, left, middle, middle + 1, right);
}
The main part of the program. Read
the input array, run the merge sort that counts the number of inversions swaps.
while(scanf("%d",&n),n)
{
m = new int[n];
for(swaps = i = 0; i < n; i++) scanf("%d",&m[i]);
mergeSort(m, 0, n -
1);
printf("%lld\n",swaps);
delete[] m;
}
Realization with sort function
#include <cstdio>
#include <string>
#include <vector>
#include <algorithm>
#define MAX 500001
using namespace
std;
int m[MAX];
int n, i, j;
long long
swaps;
void merge(int
left, int middle, int
right)
{
int i = left,
j = middle + 1;
while((i
<= middle) && (j <= right))
{
if (m[i]
<= m[j])
i++;
else
{
j++;
swaps += middle - i + 1;
}
}
sort(m + left, m + right + 1);
}
void mergeSort(int
left, int right)
{
if (left <
right)
{
int middle
= (left + right) / 2;
mergeSort(left,middle);
mergeSort(middle+1,right);
merge(left, middle, right);
}
}
int main(void)
{
while(scanf("%d",&n),n)
{
for(swaps =
i = 0; i < n; i++) scanf("%d",&m[i]);
mergeSort(0, n - 1);
printf("%lld\n",swaps);
}
return 0;
}